1545 找出第 N 个二进制字符串中的第 K 位(递归)
本文共 1561 字,大约阅读时间需要 5 分钟。
1. 问题描述:
给你两个正整数 n 和 k,二进制字符串 Sn 的形成规则如下:
S1 = "0"- 当
i > 1时,Si = Si-1 + "1" + reverse(invert(Si-1))
其中 + 表示串联操作,reverse(x) 返回反转 x 后得到的字符串,而 invert(x) 则会翻转 x 中的每一位(0 变为 1,而 1 变为 0)
例如,符合上述描述的序列的前 4 个字符串依次是:S1 = "0"S2 = "011"S3 = "0111001"S4 = "011100110110001"
请你返回 Sn 的 第 k 位字符 ,题目数据保证 k 一定在 Sn 长度范围以内。
示例 1:
输入:n = 3, k = 1
输出:"0" 解释:S3 为 "0111001",其第 1 位为 "0"示例 2:
输入:n = 4, k = 11
输出:"1" 解释:S4 为 "011100110110001",其第 11 位为 "1"示例 3:
输入:n = 1, k = 1
输出:"0"示例 4:
输入:n = 2, k = 3
输出:"1"提示:
1 <= n <= 201 <= k <= 2n - 1
2. 思路分析:
从题目中可以知道,第k个位置要不就是0要不就是1,所以我们的任务是求解出第k位到底是落在哪一个的位置上面,比如n = 3, S3 = "0111001",S3的中间位置为第4个位置,所以第4位肯定是"1"的,而且无论n等于几它的中间位置都是1的,所以这个位置是最好确定的,判断出mid == k直接返"1"即可,假如中间位置mid > k说明我们的答案是mid的左边,所以应该是往mid左边找,这个时候应该是n减小1的,也就是往S2里找,假如mid < k说明答案是在mid的右边,而我们知道左边与右边其实可以看做是对称的,我们可以计算出在右边的位置映射到左边的位置然后对字符进行取反即可,然后继续往n - 1也就是S2进行寻找
比如n = 3, k = 5,S3 = "0111001",k = 5对应mid的左边位置为 8 - 5 = 3也就是对应左边的第三位的字符然后对其取反就是答案了
基于上面的分析我们知道可以使用递归的思路去解决,根据当前的mid位置决定递归左边还是右边,当mid == k时我们返回"1",当mid > k时,我们通过移位运算计算出在左边对应的位置,1 << n - k即为左边的位置,然后向前一个n - 1的数字进行递归,当mid < k时候那么我们应该是直接往前一个n - 1的数字进行递归即可:因为答案就在n - 1的前面位置(移位的操作可以根据具体的例子来写出对应的表达式:n = 3, k = 5那么(1 << 3) - 5 = 3))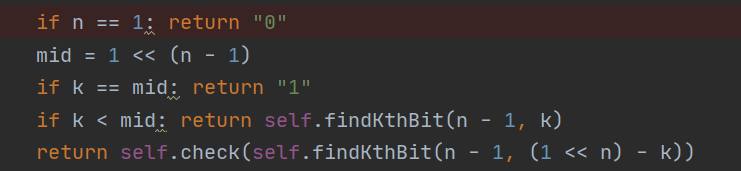
每一次都是缩小一个规模进行递归,也就是往n - 1进行递归
3. 代码如下:
class Solution: def check(self, c: str): if c == "0": return "1" else: return "0" def findKthBit(self, n: int, k: int) -> str: if n == 1: return "0" mid = 1 << (n - 1) if k == mid: return "1" if k < mid: return self.findKthBit(n - 1, k) return self.check(self.findKthBit(n - 1, (1 << n)- k))
转载地址:http://vmgr.baihongyu.com/
你可能感兴趣的文章